- Objectivos de aprendizagem
- Exemplo 9
- Exemplo 10
- Exemplo 11
- Exemplo 12
- Exemplo 13
- Exemplo 14
- A química está em todo o lado: Respirar
- Principais conclusões
- Exercícios
Objectivos de aprendizagem
- Aprender a lei dos gases ideais.
- Aplicar a lei dos gases ideais a qualquer conjunto de condições de um gás.
- Aplicar a lei dos gases ideais a problemas de volumes molares, densidade e estequiometria.
Até agora, todas as leis dos gases que considerámos exigiram que o gás alterasse as suas condições; depois previmos uma alteração resultante numa das suas propriedades. Existem leis dos gases que relacionam as propriedades físicas de um gás num determinado momento?
Considerar uma nova extensão da lei dos gases combinados para incluir n Por analogia com a lei de Avogadro, n está posicionado no denominador da fração, oposto ao volume. Assim
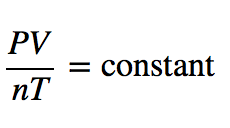
Como a pressão, o volume, a temperatura e a quantidade são as únicas quatro propriedades físicas independentes de um gás, a constante na equação acima é verdadeiramente uma constante; de facto, como não precisamos de especificar a identidade de um gás para aplicar as leis dos gases, esta constante é a mesma para todos os gases. R , pelo que a equação anterior se escreve como
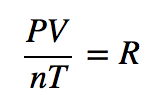
que normalmente é reordenado como
PV = nRT
Esta equação é designada por lei dos gases ideais e relaciona as quatro propriedades independentes de um gás em qualquer momento. A constante R O seu valor depende das unidades utilizadas para expressar a pressão e o volume. Tabela 6.1 "Valores da constante da lei dos gases ideais R " enumera os valores numéricos de R .
Tabela 6.1 Valores da constante da lei dos gases ideais R
| Valor numérico | Unidades |
|---|---|
| 0.08205 | L-atm/mol-K |
| 62.36 | L-torr/mol-K = L-mmHg / mol-K |
| 8.314 | J/mol-K |
A lei dos gases ideais é utilizada como qualquer outra lei dos gases, tendo em atenção as unidades e certificando-se de que a temperatura é expressa em kelvins, a lei dos gases ideais não exige uma alteração das condições de uma amostra de gás A lei dos gases ideais implica que, se conhecermos três das propriedades físicas de um gás, podemos calcular a quarta propriedade.
Exemplo 9
Uma amostra de 4,22 mol de Ar tem uma pressão de 1,21 atm e uma temperatura de 34°C. Qual é o seu volume?
Solução
O primeiro passo é converter a temperatura em kelvins:
34 + 273 = 307 K
Agora podemos substituir as condições na lei dos gases ideais:
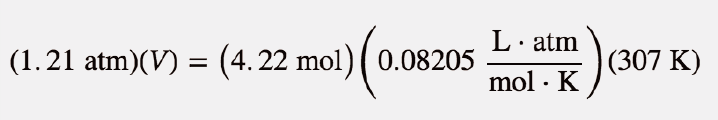
A unidade atm está no numerador de ambos os lados, pelo que se anula. No lado direito da equação, as unidades mol e K aparecem no numerador e no denominador, pelo que também se anulam. A única unidade que resta é L, que é a unidade de volume que procuramos. Isolamos a variável volume dividindo ambos os lados da equação por 1,21:
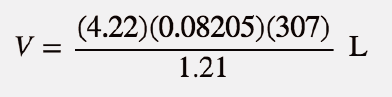
Resolvendo então para o volume, obtemos
V = 87.9 L
Teste-se a si próprio
Uma amostra de 0,0997 mol de O 2 tem uma pressão de 0,692 atm e uma temperatura de 333 K. Qual é o seu volume?
Resposta
3.94 L
Exemplo 10
A uma dada temperatura, 0,00332 g de Hg na fase gasosa tem uma pressão de 0,00120 mmHg e um volume de 435 L. Qual é a sua temperatura?
Solução
Não nos é dado o número de moles de Hg diretamente, mas é-nos dada uma massa. Podemos utilizar a massa molar de Hg para converter para o número de moles.
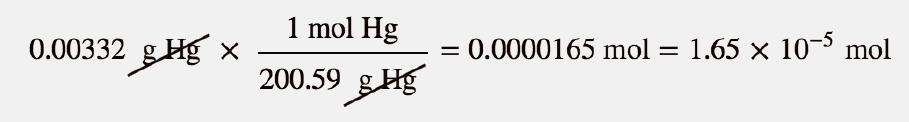
A pressão é dada em unidades de milímetros de mercúrio. Podemos converter esse valor para atmosferas ou usar o valor da constante dos gases ideais que inclui a unidade mmHg. Vamos escolher a segunda opção. Substituindo na lei dos gases ideais,
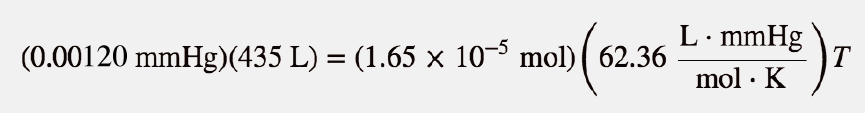
As unidades mmHg, L e mol anulam-se, deixando a unidade K, a unidade de temperatura. Isolamento T sozinho de um lado, obtemos
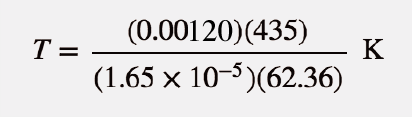
Resolvendo então para K, obtemos
T = 507 K
Teste-se a si próprio
Para uma amostra de 0,00554 mol de H 2 , P = 23,44 torr e T = 557 K. Qual é o seu volume?
Resposta
8.21 L
A lei dos gases ideais também pode ser utilizada em problemas de estequiometria.
Exemplo 11
Qual o volume de H 2 é produzido a 299 K e 1,07 atm quando 55,8 g de Zn metálico reagem com HCl em excesso?
Zn(s) + 2 HCl(aq) → ZnCl 2 (aq) + H 2 (g)
Solução
Aqui temos um problema de estequiometria em que precisamos de encontrar o número de moles de H 2 Em seguida, podemos utilizar a lei dos gases ideais, com a temperatura e a pressão dadas, para determinar o volume de gás produzido. Em primeiro lugar, o número de moles de H 2 é calculado:
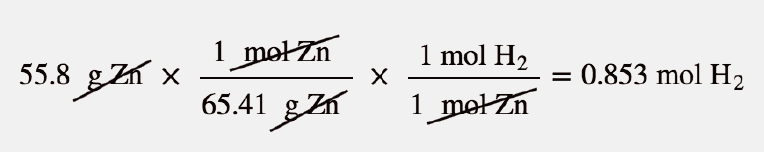
Agora que sabemos o número de moles de gás, podemos usar a lei dos gases ideais para determinar o volume, dadas as outras condições:
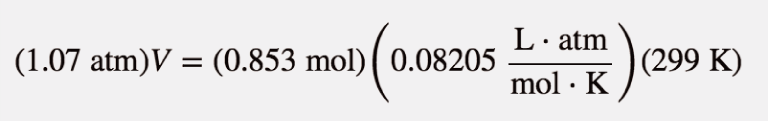
Todas as unidades se anulam exceto L, para volume, o que significa
V = 19.6 L
Teste-se a si próprio
Que pressão de HCl é gerada se 3,44 g de Cl 2 reagem em 4,55 L a 455 K?
H 2 (g) + Cl 2 (g) → 2HCl(g)
Resposta
0,796 atm
Já deve ser óbvio que algumas propriedades físicas dos gases dependem fortemente das condições. O que precisamos é de um conjunto de condições padrão para que as propriedades dos gases possam ser corretamente comparadas entre si. A temperatura e pressão padrão (STP) é definida como exatamente 100 kPa de pressão (0,986 atm) e 273 K (0°C). Para simplificar, utilizaremos 1 atm como pressão padrão. Definição de STPpermite-nos comparar mais diretamente as propriedades dos gases que diferem entre si.
Uma propriedade partilhada entre os gases é o volume molar. O volume molar é o volume de 1 mol de um gás. À temperatura ambiente, o volume molar de um gás pode ser facilmente determinado utilizando a lei dos gases ideais:
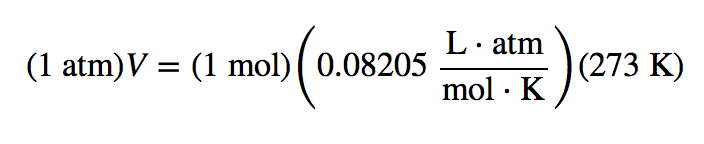
Todas as unidades se anulam, exceto L, a unidade de volume. Assim
V = 22.4 L
Note-se que não especificámos a identidade do gás; especificámos apenas que a pressão é de 1 atm e a temperatura é de 273 K. Isto permite uma aproximação muito útil: qualquer gás à temperatura ambiente tem um volume de 22,4 L por mole de gás Este volume molar é um fator de conversão útil em problemas de estequiometria se as condições estiverem ao STP. Se as condições não estiverem ao STP, um volume molar de 22,4 L/mol não é aplicável. No entanto, se as condições não estiverem ao STP, a lei dos gases combinados pode ser usada para calcular o volume do gás ao STP; então os 22,4Pode ser utilizado o volume molar L/mol.
Figura 6.3 Volume molar
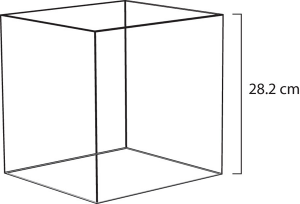
Uma mole de gás à temperatura ambiente ocupa 22,4 L, o volume de um cubo com 28,2 cm de lado.
Exemplo 12
Quantos moles de Ar estão presentes em 38,7 L à temperatura ambiente?
Solução
Podemos utilizar o volume molar, 22,4 L/mol, como fator de conversão, mas temos de inverter a fração para que as unidades L se anulem e as unidades mol sejam introduzidas:
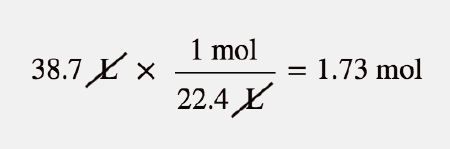
Teste-se a si próprio
Que volume tem 4,87 mol de Kr no ponto de equilíbrio?
Resposta
109 L
Exemplo 13
Qual o volume de H 2 é produzido à temperatura ambiente quando 55,8 g de Zn metálico reagem com HCl em excesso?
Zn(s) + 2 HCl(aq) → ZnCl 2 (aq) + H 2 (g)
Solução
Este é um problema de estequiometria com uma diferença: precisamos de usar o volume molar de um gás à temperatura ambiente para determinar a resposta final. A primeira parte do cálculo é a mesma que num exemplo anterior:
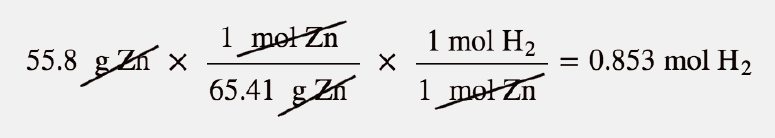
Agora podemos usar o volume molar, 22,4 L/mol, porque o gás está à temperatura ambiente:
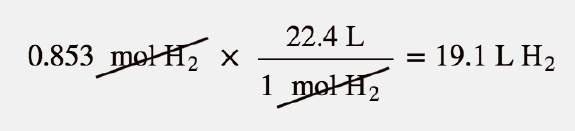
Alternativamente, poderíamos ter aplicado o volume molar como um terceiro fator de conversão no cálculo original da estequiometria.
Teste-se a si próprio
Que volume de HCl é gerado se 3,44 g de Cl 2 estão a reagir em STP?
H 2 (g) + Cl 2 (g) → 2 HCl(g)
Resposta
2.17 L
A lei dos gases ideais também pode ser utilizada para determinar as densidades dos gases. Recorde-se que a densidade é definida como a massa de uma substância dividida pelo seu volume:
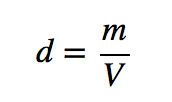
Suponha que tem exatamente 1 mol de um gás. Se souber a identidade do gás, pode determinar a massa molar da substância. Utilizando a lei dos gases ideais, pode também determinar o volume desse mol de gás, utilizando quaisquer que sejam as condições de temperatura e pressão. Em seguida, pode calcular a densidade do gás utilizando
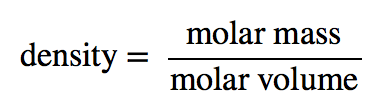
Exemplo 14
Qual é a densidade de N 2 a 25°C e 0,955 atm?
Solução
Primeiro, temos de converter a temperatura em kelvins:
25 + 273 = 298 K
Se assumirmos exatamente 1 mol de N 2 , então sabemos a sua massa: 28,0 g. Usando a lei dos gases ideais, podemos calcular o volume:
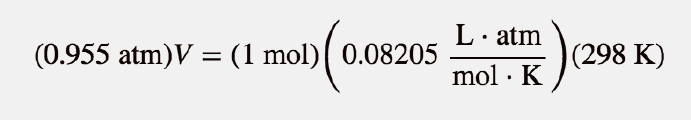
Todas as unidades se anulam, exceto L, a unidade de volume. Assim
V = 25.6 L
Conhecendo a massa molar e o volume molar, podemos determinar a densidade de N 2 nestas condições:
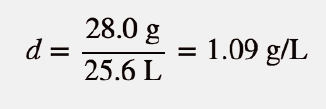
Teste-se a si próprio
Qual é a densidade do CO 2 a uma pressão de 0,0079 atm e 227 K? (Estas são as condições atmosféricas aproximadas em Marte).
Resposta
0,019 g/L
A química está em todo o lado: Respirar
A respiração (mais propriamente designada por respiração ) é o processo pelo qual aspiramos ar para os pulmões, de modo a que o nosso corpo possa absorver o oxigénio do ar. Apliquemos as leis dos gases à respiração.
Começamos por considerar a pressão. Puxamos o ar para os pulmões porque o diafragma, um músculo por baixo dos pulmões, se move para baixo para reduzir a pressão nos pulmões, fazendo com que o ar externo entre para encher o volume de baixa pressão. Expulsamos o ar porque o diafragma empurra contra os pulmões, aumentando a pressão dentro dos pulmões e forçando o ar de alta pressão para fora. Quais são as mudanças de pressão envolvidas?Na verdade, em condições normais, uma diferença de pressão de apenas 1 ou 2 torr faz-nos inspirar e expirar.
Figura 6.4 Mecânica da respiração
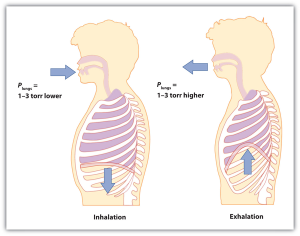
A respiração envolve diferenças de pressão entre o interior dos pulmões e o ar exterior, diferenças essas que são de apenas alguns torr.
Uma respiração normal é de cerca de 0,50 L. Se a temperatura ambiente é de cerca de 22°C, então o ar tem uma temperatura de cerca de 295 K. Sendo a pressão normal de 1,0 atm, quantos moles de ar absorvemos por cada respiração? A lei dos gases ideais dá-nos uma resposta:
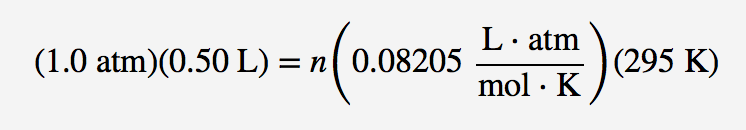
Resolvendo para o número de moles, obtemos
n = 0,021 mol de ar
Isto acaba por ser cerca de 0,6 g de ar por respiração - não é muito, mas é o suficiente para nos manter vivos.
Principais conclusões
- A lei dos gases ideais relaciona as quatro propriedades físicas independentes de um gás em qualquer momento.
- A lei dos gases ideais pode ser utilizada em problemas de estequiometria em que as reacções químicas envolvem gases.
- A temperatura e pressão normais (STP) são um conjunto útil de condições de referência para comparar outras propriedades dos gases.
- À temperatura ambiente, os gases têm um volume de 22,4 L por mole.
- A lei dos gases ideais pode ser utilizada para determinar as densidades dos gases.
Exercícios
O que é a lei dos gases ideais? Qual é o significado de R ?
Porque é que R têm valores numéricos diferentes (ver Quadro 6.1 "Valores da constante da lei dos gases ideais R ")?
Uma amostra de gás tem um volume de 3,91 L, uma temperatura de 305 K e uma pressão de 2,09 atm. Quantos moles de gás estão presentes?
Uma amostra de 3,88 mol de gás tem uma temperatura de 28°C e uma pressão de 885 torr. Qual é o seu volume?
Uma amostra de 0,0555 mol de Kr tem uma temperatura de 188°C e um volume de 0,577 L. Qual é a sua pressão?
Se 1,000 mol de gás tem um volume de 5,00 L e uma pressão de 5,00 atm, qual é a sua temperatura?
Uma amostra de 7,55 g de He tem um volume de 5.520 mL e uma temperatura de 123°C. Qual é a sua pressão em torr?
Uma amostra de 87,4 g de Cl 2 tem uma temperatura de -22°C e uma pressão de 993 torr. Qual é o seu volume em mililitros?
Uma amostra de Ne tem uma pressão de 0,772 atm e um volume de 18,95 L. Se a sua temperatura é de 295 K, que massa está presente na amostra?
Uma lâmpada de mercúrio contém 0,0055 g de vapor de Hg num volume de 15,0 mL. Se a temperatura de funcionamento for 2.800 K, qual é a pressão do vapor de mercúrio?
O oxigénio é um produto da decomposição do óxido de mercúrio(II):
2 HgO(s) → 2 Hg(ℓ) + O 2 (g)
Qual o volume de O 2 é formado pela decomposição de 3,009 g de HgO se o gás tiver uma pressão de 744 torr e uma temperatura de 122°C?
O óxido de lítio é utilizado para absorver o dióxido de carbono:
Li 2 O(s) + CO 2 (g) → Li 2 CO 3 (s)
Qual o volume de CO 2 pode 6,77 g de Li 2 O absorver se o CO 2 a pressão é de 3,5 × 10-4 atm e a temperatura é de 295 K?
Qual é o volume de 17,88 mol de Ar à temperatura ambiente?
Quantos moles estão presentes em 334 L de H 2 em STP?
Quantos litros de CO 2 à temperatura ambiente são produzidos a partir de 100,0 g de C 8 H 18 A fórmula aproximada da gasolina?
2 C 8 H 18 (ℓ) + 25 O 2 (g) → 16 CO 2 (g) + 18 H 2 O(ℓ)
Quantos litros de O 2 à temperatura ambiente são necessários para queimar 3,77 g de butano de um isqueiro descartável?
2 C 4 H 10 (g) + 13 O 2 (g) → 8 CO 2 (g) + 10 H 2 O(ℓ)
Qual é a densidade de cada gás a STP?
a) Ele
b) Ne
c) Ar
d) Kr
18) Qual é a densidade de cada gás à temperatura ambiente?
a) H 2
b) O 2
c) N 2
19) Qual é a densidade do SF 6 a 335 K e 788 torr?
20. Qual é a densidade do He a -200°C e 33,9 torr?
Respostas
1. A lei dos gases ideais é PV = nRT . R é a constante da lei dos gases ideais, que relaciona as outras quatro variáveis.
3. 0,327 mol
5. 3,64 atm
7. 8.440 torr
9. 12.2 g
11. 0.230 L
13. 401 L
15. 157 L
17.
a) 0,179 g/L
b) 0,901 g/L
c) 1,78 g/L
d) 3,74 g/L
19. 5,51 g/L